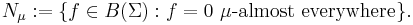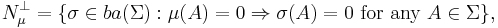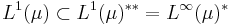ba space

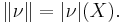In mathematics, the ba space $ba(\Sigma)$ of an algebra of sets $\Sigma$ is the Banach space consisting of all bounded and finitely additive measures on $\Sigma$ . The norm is defined as the variation, that is $\|\nu\|=|\nu|(X).$ (Dunford & Schwartz 1958, IV.2.15)

If Σ is a sigma-algebra, then the space 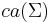$ca(\Sigma)$ is defined as the subset of 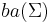$ba(\Sigma)$ consisting of countably additive measures. (Dunford & Schwartz 1958, IV.2.16)

If X is a topological space, and Σ is the sigma-algebra of Borel sets in X, then 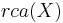$rca(X)$ is the subspace of 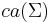$ca(\Sigma)$ consisting of all regular Borel measures on X. (Dunford & Schwartz 1958, IV.2.17)

Properties

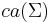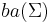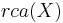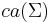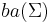All three spaces are complete (they are Banach spaces) with respect to the same norm defined by the total variation, and thus $ca(\Sigma)$ is a closed subset of $ba(\Sigma)$ , and $rca(X)$ is a closed set of $ca(\Sigma)$ for Σ the algebra of Borel sets on X. The space of simple functions on $\Sigma$ is dense in $ba(\Sigma)$ .

The ba space of the power set of the natural numbers, ba(2^N), is often denoted as simply 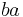$ba$ and is isomorphic to the dual space of the ℓ^∞ space.

Let B(Σ) be the space of bounded Σ-measurable functions, equipped with the uniform norm. Then ba(Σ) = B(Σ)* is the continuous dual space of B(Σ). This is due to Hildebrandt (1934) and Fichtenholtz & Kantorovich (1934). This is a kind of Riesz representation theorem which allows for a measure to be represented as a linear functional on measurable functions. In particular, this isomorphism allows one to define the integral with respect to a finitely additive measure (note that the usual Lebesgue integral requires countable additivity). This is due to Dunford & Schwartz (1958), and is often used to define the integral with respect to vector measures (Diestel & Uhl 1977, Chapter I), and especially vector-valued Radon measures.

The topological duality ba(Σ) = B(Σ)* is easy to see. There is an obvious algebraic duality between the vector space of all finitely additive measures σ on Σ and the vector space of simple functions. It is easy to check that the linear form induced by σ is continuous in the sup-norm iff σ is bounded, and the result follows since a linear form on the dense subspace of simple functions extends to an element of B(Σ)* iff it is continuous in the sup-norm.

If Σ is a sigma-algebra and μ is a sigma-additive positive measure on Σ then the Lp space L^∞(μ) endowed with the essential supremum norm is by definition the quotient space of B(Σ) by the closed subspace of bounded μ-null functions:

$N_\mu:=\{f\in B(\Sigma)�: f = 0 \ \mu\text{-almost everywhere} \}.$

The dual Banach space L^∞(μ)* is thus isomorphic to

$N_\mu^\perp=\{\sigma\in ba(\Sigma)�: \mu(A)=0\Rightarrow \sigma(A)= 0 \text{ for any }A\in\Sigma\},$

i.e. the space of finitely additive signed measures on Σ that are absolutely continuous with respect to μ (μ-a.c. for short).

When the measure space is furthermore sigma-finite then L^∞(μ) is in turn dual to L¹(μ), which by the Radon–Nikodym theorem is identified with the set of all countably additive μ-a.c. measures. In other words the inclusion in the bidual

$L^1(\mu)\subset L^1(\mu)^{**}=L^{\infty}(\mu)^*$

is isomorphic to the inclusion of the space of countably additive μ-a.c. bounded measures inside the space of all finitely additive μ-a.c. bounded measures.

References

Diestel, Joseph (1984), Sequences and series in Banach spaces, Springer-Verlag, ISBN 0-387-90859-5, OCLC 9556781 .
Diestel, J.; Uhl, J.J. (1977), Vector measures, Mathematical Surveys, 15, American Mathematical Society .
Dunford, N.; Schwartz, J.T. (1958), Linear operators, Part I, Wiley-Interscience .
Hildebrandt, T.H. (1934), "On bounded functional operations", Transactions of the American Mathematical Society 36 (4): 868–875, doi:10.2307/1989829, JSTOR 1989829 .
Fichtenholz, G; Kantorovich, L.V. (1934), "Sur les opérationes linéaires dans l'espace des fonctions bornées", Studia Mathematica 5: 69–98 .
Yosida, K; Hewitt, E (1952), "Finitely additive measures", Transactions of the American Mathematical Society 72 (1): 46–66, doi:10.2307/1990654, JSTOR 1990654 .